Merge Sort: A Deep Dive into the Divide and Conquer Sorting Algorithm

Written By:

Nestor Rubio

Last Updated:

December 11th, 2023

So you’re looking into sorting algorithms and came across one of the most popular topics in the area? This is the place to be then because in this piece, we will explore the topic of the Merge Sort algorithm in every sense from abstract to in-code examples and will even discuss why this tool is so popular in any computer science education. Whether you’re new to the world of Merge Sort or have experience and are seeking a refresher, I hope to provide everything you need and more, below.

Programming languages used in this post include: Java, C, Python, Go, and JavaScript

The Overview of Merge Sort

The big thing to know is that Merge Sort at its core is a sorting algorithm, with its primary function being to sort a collection of items. How it does this is the interesting and (in my opinion) cool part.

When asked to summarize Merge Sort I go with something along the lines of :

Merge Sort is a sorting algorithm which works by taking an array of items and using the principle of divide and conquer to repetitively sort halves of the array.

I feel that this alone does it justice because we can best understand a merge sort by analyzing the steps involved in implementing it and we will see the key parts of the description above mentioned in those steps.

1. Divide the input array into two halves of the array
2. Sort each half of the array
3. Conquer the problem by merging the sorted halves of the array back together in a way that preserves the order and results in a single sorted array

You may be looking at those three steps and be asking “How does each half get sorted?”. That is a valid question. One that has a pretty cool answer.

If we view the problem as repeating step 1 and 2 until we are sorting two halves, each of one item, then we get to a nice point when each half is trivially sorted because it has only one item. From here, we can start step 3 which means merging the two arrays into one sorted array. This pattern will continue to merging halves of an array, each one being larger than the last until we reach the original array size. Once here, we merge the two halves, making a final, sorted array.

The visual below shows this process in full on an array of size 10. It displays the steps in a top-down fashion meaning the top is the array’s original state and the end is the sorted array, making each phase in between a different step in the sorting. I’m hoping it helps solidify each step and how it makes the full sorting of an array using Merge Sort.

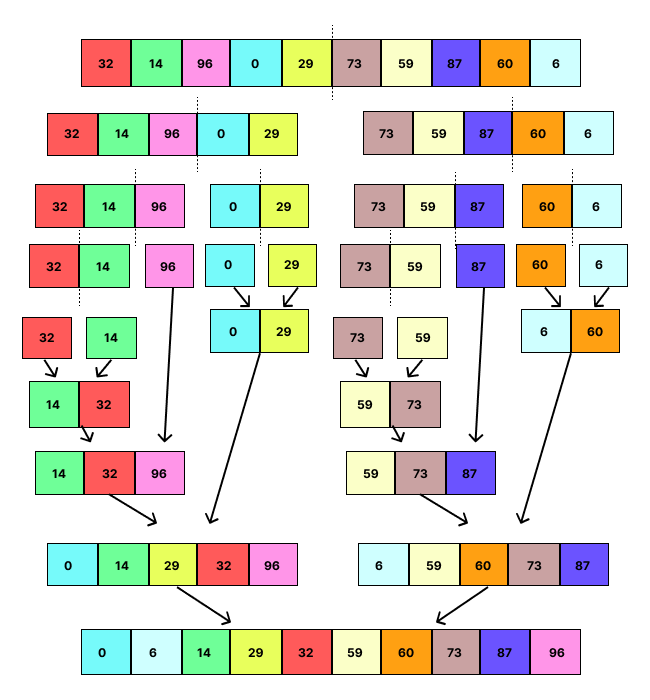
The principle of Divide and Conquer which creates the foundation for this sorting algorithm opens the door for a cool way for this to be implemented which is recursion. To provide a quick description of recursion, it is is the method of solving a problem by having a function call itself but with a smaller version of the problem until an overall solution can be built. We see that in the above because we keep dividing the array into small pieces until a base case of one item is found and from there we can keep merging them all on the way back up to the overall array. A recursive implementation showcases how Merge Sort can be employed within itself, allowing for an efficient solution to the sorting problem.

Algorithm Analysis

If you have not been introduced to the world of Big O Notation and algorithm analysis, there’s no worries because you can read more about it in my post here as an introduction. It’s okay if you need to skip this section and come back to it later. Learning is not a linear path.

When looking at this sorting algorithm, we need to know some things about it. How long can we expect it to take to complete? How much extra memory should we expect to need in order to complete this sort? Let’s explore the answers to these questions.

Time Complexity

Luckily, the runtime of this can be described pretty concisely with the following:

We can reach the O(N*log(N)) result for each of these cases by considering some aspects of the narrative described before. First, the

All three cases having the same time complexity actually leads to a fun fact which is that this is a special case where we can refer to the runtime as θ(N*log(N)) which can be read as “Big Theta N times log N”. Big Theta notation is seen as the sweet spot when the best, average, and worst case all line up meaning no matter what, the number of operations will be the same for any two arrays of the same size N. This makes sense considering the base case or point of no more iterations is when the array being sorted is of only one element. No matter what, we need to break the array down into those pieces anyways, there is no way to avoid it with this algorithm.

Personal Note: We could get into picky specific cases like checking if the array is sorted before each thing but this can get extremely expensive computationally and is more likely than not going to result in pointless O(N) operations since if we can assume a sorted array, we wouldn’t need a sorting algorithm.

Space Complexity

The space complexity can be seen in the description of the sorting process. The fact that we need to create a temporary array to add the sorted items into, we can infer that the largest any extra array can get is of the same size as the array. Thus, if N items are passed into the array, the largest extra array required would also contain N elements. This way, we can determine the space complexity is O(N), where N represents the number of items in the list being sorted.

If you consider the recursive approach and can visualize your function call stack as having a max depth of log(N), you could be tempted to call the space complexity as O(N*log(N)). This would be missing one key fact which is that not all log(N) function calls will have the extra array made at the same time. This means that even if the depth of the call stack is at its lowest, the size of the largest possible array still overshadows the call stack depth. This means we could see the space complexity as O(N+log(N)) which can then be simplified to O(N) as it is the dominant factor as N grows.

Bottom line is space complexity can be summed up as O(N) mainly due to the extra array of the same size as the sorted array which is needed to combine the two sorted halves of the array.

Programming Merge Sort

Here are examples of ways to program the Merge Sort in both the recursive and iterative approaches. I recommend trying to understand both in at least one language because that can help you gain an even deeper understanding of how Merge Sort works in theory and in practice.

Recursive Approach

import java.io.*;
import java.util.*;

public class MergeSort {
  private static final int MAX_SIZE = 10;
  private static final int MAX_VALUE = 100;

  // method to merge two subarrays into main array based on indeces defining it
  private static void merge(int[] arr, int left, int mid, int right) {
    // get number of elements on left and right
    int numElementsLeft = mid - left + 1;
    int numElementsRight = right - mid;
    
    // create arrays of appropriate size
    int[] leftArray = new int[numElementsLeft];
    int[] rightArray = new int[numElementsRight];
    
    // fill temp arrays
    for(int i = 0; i < numElementsLeft; i++) {
      leftArray[i] = arr[left + i];
    }
    for(int i = 0; i < numElementsRight; i++) {
      rightArray[i] = arr[mid + i + 1];
    }
    
    // merge arrays in sorted order for so long as both arrays have elements
    int leftIndex = 0, rightIndex = 0, mergedIndex = left;

    while(leftIndex < numElementsLeft && rightIndex < numElementsRight) {
      if(leftArray[leftIndex] <= rightArray[rightIndex]) {
        arr[mergedIndex] = leftArray[leftIndex];
        leftIndex++; 
      } else {
        arr[mergedIndex] = rightArray[rightIndex];
        rightIndex++;
      }
      mergedIndex++;
    }

    // ensure all elements from both arrays get copied to arr
    // ++ notation can be seen as "use current value and THEN increment it by one"
    while(leftIndex < numElementsLeft) {
      arr[mergedIndex++] = leftArray[leftIndex++];
    }
    while(rightIndex < numElementsRight) {
      arr[mergedIndex++] = rightArray[rightIndex++];
    }

    // Java garbage collector can handle freeing the temporary memory we allocated
  }

  // actual recursive merge sort method
  private static void mergeSort(int[] arr, int left, int right) {
    if(left >= right) {
      return;
    }
    // way of calculating mid that saves some chance from integer overflow in extremely large arrays
    int mid = left + (right - left) / 2;

    mergeSort(arr,left,mid);
    mergeSort(arr,mid + 1,right);

    merge(arr,left,mid,right);
  }

  // gateway method to abstract the need for a user to provide the initial indeces
  public static void mergeSortRecursive(int[] array) {
    mergeSort(array,0,array.length - 1);
  }

  // main method to run our program with
  public static void main(String[] args) {
    int[] array = new int[MAX_SIZE];

    for(int i = 0; i< MAX_SIZE; i++) {
      array[i] = (int)(Math.random() * MAX_VALUE);
    }

    System.out.println("Before Merge: " + Arrays.toString(array));
    
    mergeSortRecursive(array);
    
    System.out.println("After Merge: " + Arrays.toString(array));
  }
}

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

// global variable for array length
#define ARR_LEN 10
#define MAX_VALUE 100

// function used to merge the list based on a left, middle, and right index
void merge(int arr[], int l, int m, int r) {
  int i, j, k;

  // get number of elements on left and right side
  int leftElementsCount = m - l + 1;
  int rightElementsCount = r - m;

  // make temporary arrays, populating them with the values from the original array
  int *leftArray = malloc(leftElementsCount * sizeof(int));
  int *rightArray = malloc(rightElementsCount * sizeof(int));
  for (i = 0; i < leftElementsCount; i++) {
    leftArray[i] = arr[l + i];
  }
  for (j = 0; j < rightElementsCount; j++) {
    rightArray[j] = arr[m + 1 + j];
  }

  // reset helper variables
  i = 0;
  j = 0;
  k = l;
    
  // merge the temporary arrays back into the original array doing comparison to see which value to insert at that point UNTIL one of the temporary arrays runs out of values
  while (i < leftElementsCount && j < rightElementsCount) {
    if (leftArray[i] <= rightArray[j]) {
      arr[k] = leftArray[i];
      i++;
      k++;
    } else {
      arr[k] = rightArray[j];
      j++;
      k++;
    }
  }

  // make sure all remaining elements of the temporary arrays are merged into the array, we can assume all remaining values will be in sorted order due to the recursive nature of merge sort
  while (i < leftElementsCount) {
    arr[k] = leftArray[i];
    i++;
    k++;
  }
  while (j < rightElementsCount) {
    arr[k] = rightArray[j];
    j++;
    k++;
  }

  // free the temporary arrays to avoid memory leaks
  free(leftArray);
  free(rightArray);
}

// abstracted function so users don't deal with inputting left and right indeces
void _mergeSort(int arr[], int left, int right) {
  // base case: if leftmost value of array and rightmost value are same or crossed over, then we know there is nothing to sort
  if (left >= right) {
    return;
  }
  // define middle index
  int mid = (left + right) / 2;

  // divide and conquer each half of the array
  _mergeSort(arr, left, mid);
  _mergeSort(arr, mid + 1, right);

  // merge both halves together since we can assume that both halves are now sorted
  merge(arr, left, mid, right);
}

// accessible "gateway" function allowing merge sort to begin
void mergeSort(int arr[]) { _mergeSort(arr, 0, ARR_LEN - 1); }

// helper function for printing arrays in a nice way
void printArray(int *array, char *label) {
  printf("%s[", label);
  for (int i = 0; i < ARR_LEN - 1; i++) {
    printf("%d, ", array[i]);
  }
  printf("%d]\n", array[ARR_LEN - 1]);
}

// main function
int main(int argv, char **args) {
  // implement seed for random number generation
  srand(time(NULL));

  // create array of length ARR_LEN with random ints
  int *array = malloc(ARR_LEN * sizeof(int));
  for (int i = 0; i < ARR_LEN; i++) {
    array[i] = rand() % MAX_VALUE;
  }

  // print array before sorting
  printArray(array, "Before Sorting: ");

  // sort array
  mergeSort(array);

  // print array after merging
  printArray(array, "After Sorting: ");

  // free array to avoid memory leaks
  free(array);
}

import random
      
# function to merge a literal left and right array
def merge(left, right):
  # declare merged array
  merged = []
  # declare indeces for left and right
  left_index, right_index = 0, 0
  # while both subarrays have values, keep adding the smallest front value to merged array
  while left_index < len(left) and right_index < len(right):
    if(left[left_index] <= right[right_index]):
      merged.append(left[left_index])
      left_index += 1
    else:
      merged.append(right[right_index])
      right_index += 1

  # add all remaining values from left and right array to merged
  merged += left[left_index:] + right[right_index:]

  # return merged array
  return merged

def merge_sort(array):
  # if trivially sorted, return the array
  if len(array) <= 1:
    return array
  # mid index is length of the array divided by 2 using floor division
  # floor division is just rounding down no matter what. 3.95 -> 3
  mid = len(array) // 2
  # left array is subarray from index 0 to mid - 1
  left = array[:mid]
  # right array is subarray from index mid to the end of the array
  right = array[mid:]

  # recursively merge sort the arrays
  left = merge_sort(left)
  right = merge_sort(right)

  # return merged halves of the array
  return merge(left,right)
  
# main code to be ran
# name == main thing is saying 'if I ran this specific file, then execute this function'
if __name__ == "__main__":
  # test array is a 10 element array of random integers from 0 to 100 
  my_array = [random.randint(0,100) for _ in range(10)]
  
  # sort the array
  sorted_list = merge_sort(my_array)
  
  # print our successfully sorted array
  print(sorted_list)
  

package main

import (
	"fmt"
	"math"
	"math/rand"
	"time"
)

func generateRandomIntegerArray(length, min, max int) []int {
  // declare seed for random number generation
  rand.Seed(time.Now().UnixNano())

  // declare the array and its length
  arr := make([]int, length)

  // insert a random int between min and max for each index
  for i := 0; i < length; i++ {
    arr[i] = rand.Intn(max - min + 1) + min
  }

  return arr
}

// function to merge two arrays together in sorted order
func merge(leftArr,rightArr []int) []int {
  // declare left and right indeces to compare values during merge
  leftIndex,rightIndex := 0,0
  
  // declare merged array
  // NOTE: make takes the arguments of ([]int, length, capacity)
  merged := make([]int, 0, len(leftArr) + len(rightArr))

  // while both arrays have values, merge in the smaller of the two leading ones
  for leftIndex < len(leftArr) && rightIndex < len(rightArr) {
    if leftArr[leftIndex] < rightArr[rightIndex] {
      merged = append(merged, leftArr[leftIndex])
      leftIndex++
    } else {
      merged = append(merged, rightArr[rightIndex])
      rightIndex++
    }
  }

  // when one array runs out of values, merge the remainder of the other array in
  for leftIndex < len(leftArr) {
    merged = append(merged, leftArr[leftIndex])
    leftIndex++
  }
  for rightIndex < len(rightArr) {
    merged = append(merged, rightArr[rightIndex])
    rightIndex++
  }

  return merged
}

// recursive function to sort an array of ints
func mergeSortRecursive(list []int) []int {
  // if trivially sorted (base case), then return the list
  if len(list) <= 1 {
    return list
  }
  // define midpoint of array using ints to make use of floor division
  mid := int(len(list) / 2)
  
  // define left and right arrays
  leftHalf := list[0:mid]
  rightHalf := list[mid:]
  
  // sort left and right arrays
  leftHalf = mergeSortRecursive(leftHalf)
  rightHalf = mergeSortRecursive(rightHalf)

  // return merged solution
  return merge(leftHalf, rightHalf)
}

func main() {
  list := generateRandomIntegerArray(10, 0, 100)

  fmt.Printf("Before sorting: %v\n", list)

  list = mergeSortRecursive(list)
  
  fmt.Printf("After sorting: %v", list)
}

// helper function for random integer array in range
function getRandomInt(min, max) {
  min = Math.ceil(min);
  max = Math.floor(max);
  
  return Math.floor(Math.random() * (max - min + 1)) + min;
}

// function to merge two halves of an array into one, returning the merged array
function merge(leftArray, rightArray) {
    // declare returned merged array
    const merged = [];
    // declare index values to iterate through left and right arrays
    let leftIndex = 0;
    let rightIndex = 0;

    // while both halves contain elements to merge, keep inserting the smaller value    
    while(leftIndex < leftArray.length && rightIndex < rightArray.length) {
        if(leftArray[leftIndex] <= rightArray[rightIndex]) {
            merged.push(leftArray[leftIndex]);
            leftIndex += 1;
        } else {
            merged.push(rightArray[rightIndex]);
            rightIndex += 1;
        }
    }
    // merge all leftover sorted values into the merged array
    while(leftIndex < leftArray.length) {
        merged.push(leftArray[leftIndex]);
        leftIndex += 1;
    }
    while(rightIndex < rightArray.length) {
        merged.push(rightArray[rightIndex]);
        rightIndex += 1;
    }
    
    return merged
}

 // recursive merge sort function
function mergeSortRecursive(array) {
    // if trivially sorted, return the array
    if(array.length <= 1) return array;
    
    // calculate mid point
    const mid = Math.floor(array.length / 2);
    
    // use slice operation to return a substring of array
    let leftHalf = array.slice(0,mid); // range is 0 to mid (excluding mid)
    let rightHalf = array.slice(mid); // range is from mid to end of list
    
    // recursively sort each half
    leftHalf = mergeSortRecursive( array.slice(0, mid) );
    rightHalf = mergeSortRecursive( array.slice(mid) );
    
    // return sorted array which is the merge of both halves
    return merge(leftHalf, rightHalf)
}

// following code is main
let list = Array.from({length: 10}, () => getRandomInt(0,100));

console.log("Before merge:",list);

list = mergeSortRecursive(list);

console.log("After merge:",list);

Iterative Approach

import java.io.*;
import java.util.*;

public class MergeSort {
  private static final int MAX_SIZE = 10;
  private static final int MAX_VALUE = 100;

  // method to merge two subarrays into main array based on indeces defining it
  private static void merge(int[] arr, int left, int mid, int right) {
    // get number of elements on left and right
    int numElementsLeft = mid - left + 1;
    int numElementsRight = right - mid;
    
    // create arrays of appropriate size
    int[] leftArray = new int[numElementsLeft];
    int[] rightArray = new int[numElementsRight];
    
    // fill temp arrays
    for(int i = 0; i < numElementsLeft; i++) {
      leftArray[i] = arr[left + i];
    }
    for(int i = 0; i < numElementsRight; i++) {
      rightArray[i] = arr[mid + i + 1];
    }
    
    // merge arrays in sorted order for so long as both arrays have elements
    int leftIndex = 0, rightIndex = 0, mergedIndex = left;

    while(leftIndex < numElementsLeft && rightIndex < numElementsRight) {
      if(leftArray[leftIndex] <= rightArray[rightIndex]) {
        arr[mergedIndex] = leftArray[leftIndex];
        leftIndex++; 
      } else {
        arr[mergedIndex] = rightArray[rightIndex];
        rightIndex++;
      }
      mergedIndex++;
    }

    // ensure all elements from both arrays get copied to arr
    // ++ notation can be seen as "use current value and THEN increment it by one"
    while(leftIndex < numElementsLeft) {
      arr[mergedIndex++] = leftArray[leftIndex++];
    }
    while(rightIndex < numElementsRight) {
      arr[mergedIndex++] = rightArray[rightIndex++];
    }

    // Java garbage collector can handle freeing the temporary memory we allocated
  }

  // method to perform an iterative merge sort
  public static void mergeSortIterative(int[] array) {
    int len = array.length;

    // length of merged current array doubles in size after each iteration
    for(int curSize = 1; curSize < len; curSize *= 2) {
      // choose starting index for inner subarrays
      for(int leftIndex = 0; leftIndex < len; leftIndex += curSize * 2) {
        // get ending and mid indeces for inner subarrays, considering the possibility of exceeding the bounds of the array in the process
        int mid = Math.min(leftIndex + curSize - 1, len - 1);
        int rightIndex = Math.min(leftIndex + curSize * 2 - 1, len - 1);

        // merge based on calculated index values
        merge(array,leftIndex, mid, rightIndex);
      }
    }
  }

  // main method to run our program with
  public static void main(String[] args) {
    int[] array = new int[MAX_SIZE];

    for(int i = 0; i< MAX_SIZE; i++) {
      array[i] = (int)(Math.random() * MAX_VALUE);
    }

    System.out.println("Before Merge: " + Arrays.toString(array));

    mergeSortIterative(array);
    
    System.out.println("After Merge: " + Arrays.toString(array));
  }
}

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

#define ARR_LEN 10
#define MAX_VAL 100

// simple min function saying "if a < b, return a otherwise return b"
int min(int a, int b) { return (a < b) ? a : b; }

// function used to merge two subarrays based on the left, right, and mid indeces defining those subarrays
void merge(int* arr, int left, int mid, int right) {
  // get number of elements for each temporary array
  int numElementsLeft = mid - left + 1;
  int numElementsRight = right - mid;

  // create temporry arrays
  int* leftArray = malloc(numElementsLeft * sizeof(int));
  int* rightArray = malloc(numElementsRight * sizeof(int));

  // fill temporary arrays with values from array
  for(int i = 0; i < numElementsLeft; i++) {
    leftArray[i] = arr[left + i];
  }
  for(int i =0; i < numElementsRight; i++) {
    rightArray[i] = arr[mid + 1 + i];
  }
  
  // merge temp array values into array
  int leftCurIndex = 0, rightCurIndex = 0, mergedCurIndex = left;

  // so long as left and right arrays have values to merge keep comparing and merging
  while(leftCurIndex < numElementsLeft && rightCurIndex < numElementsRight) {
    int leftElement = leftArray[leftCurIndex];
    int rightElement = rightArray[rightCurIndex];

    // remember we merge in the lesser value first and increment indeces accordingly
    if(leftElement <= rightElement) {
      arr[mergedCurIndex] = leftElement;
      leftCurIndex++;
    } else {
      arr[mergedCurIndex] = rightElement;
      rightCurIndex++;
    }

    mergedCurIndex++;
  }

  // ensure all leftover values get merged in
  while(leftCurIndex < numElementsLeft) {
    arr[mergedCurIndex] = leftArray[leftCurIndex];
    leftCurIndex++;
    mergedCurIndex++;
  }
  while(rightCurIndex < numElementsRight) {
    arr[mergedCurIndex] = rightArray[rightCurIndex];
    rightCurIndex++;
    mergedCurIndex++;
  }

  // free temp arrays to avoid memory leaks
  free(leftArray);
  free(rightArray);
}

void mergeSortIterative(int *arr) {
  // could get lenth another way but here we know it's ARR_LEN
  int numElements = ARR_LEN;

  // merging sub-arrays left to right in increasing size of a factor of 2. Kind of like going up the recursion stack without having to make the recursive calls to begin with
  for(int curSize = 1; curSize <= (numElements - 1); curSize *= 2) {
    // with our array size doubling and defined, time to merge the length of our current size list, starting with the leftIndex of it at each point 
    for(int leftIndex = 0; leftIndex < (numElements - 1); leftIndex += (curSize * 2)) {
      // get the midpoint of the current subarray, considering possibility of our reach being past the array size so we need to cap our mid and right at the max possible index which is n - 1
      int mid = min(leftIndex + curSize - 1, numElements - 1);
      int rightIndex = min(leftIndex + (2 * curSize) - 1, numElements - 1);

      // go ahead and merge the array based on the indeces defined
      merge(arr,leftIndex,mid,rightIndex);
    }
  }
}

// helper function for printing arrays in a nice way
void printArray(int *array, char *label) {
  printf("%s[", label);
  for (int i = 0; i < ARR_LEN - 1; i++) {
    printf("%d, ", array[i]);
  }
  printf("%d]\n", array[ARR_LEN - 1]);
}

// main function
int main(int argv, char **args) {
  // implement seed for random number generation
  srand(time(NULL));

  // create array of length ARR_LEN with random ints
  int *array = malloc(ARR_LEN * sizeof(int));
  for (int i = 0; i < ARR_LEN; i++) {
    array[i] = rand() % MAX_VAL;
  }

  // print array before sorting
  printArray(array, "Before Sorting: ");

  // sort array
  mergeSortIterative(array);

  // print array after merging
  printArray(array, "After Sorting: ");

  // free array to avoid memory leaks
  free(array);
}

import random

def merge_iterative(a, left, mid, right): 
  # get number of elements on left and right
  numElementsLeft = mid - left + 1
  numElementsRight = right - mid 
  # create temporary arrays and populate them with values form original array
  leftArray = [0] * numElementsLeft 
  rightArray = [0] * numElementsRight 
  for i in range(0, numElementsLeft): 
      leftArray[i] = a[left + i] 
  for i in range(0, numElementsRight): 
      rightArray[i] = a[mid + i + 1] 
  # indices for left, right, and original array
  curLeft, curRight, mergedIndex = 0, 0, left 
  # while left and right have values to compare, keep inserting the lowest value
  while curLeft < numElementsLeft and curRight < numElementsRight: 
      if leftArray[curLeft] <= rightArray[curRight]: 
          a[mergedIndex] = leftArray[curLeft] 
          curLeft += 1
      else: 
          a[mergedIndex] = rightArray[curRight] 
          curRight += 1
      mergedIndex += 1

  # insert all remaining sorted values into array
  while curLeft < numElementsLeft: 
      a[mergedIndex] = leftArray[curLeft] 
      curLeft += 1
      mergedIndex += 1

  while curRight < numElementsRight: 
      a[mergedIndex] = rightArray[curRight] 
      curRight += 1
      mergedIndex += 1

def merge_sort_iterative(array):
  # width of sorted subarrays to merge, starting at the trivial case at 1 element
  width = 1
  numElements = len(array)
  
  # while sorted part of array is not the same length as array
  while (width < numElements):
      # start from left index because in a recursive stack, it's the first
      # element to be confirmed as trivially sorted
      left=0;
      while (left < numElements): 
          r = min(left + (width*2 - 1), numElements - 1)         
          m = min(left + width - 1, numElements - 1)
          merge_iterative(array, left, m, r)
          left += width*2
      # doubling the width of the sorted part of the array
      width *= 2
  return array
      
# main code to be ran
# name == main thing is saying 'if I ran this specific file, then execute this function'
if __name__ == "__main__":
  # test array is a 10 element array of random integers from 0 to 100 
  my_array = [random.randint(0,100) for _ in range(10)]
  # sort the array
  #sorted_list = merge_sort(my_array)
  sorted_list = merge_sort_iterative(my_array)
  
  # print our successfully sorted array
  print(sorted_list)
  

package main

import (
	"fmt"
	"math"
	"math/rand"
	"time"
)

func generateRandomIntegerArray(length, min, max int) []int {
  // declare seed for random number generation
  rand.Seed(time.Now().UnixNano())

  // declare the array and its length
  arr := make([]int, length)

  // insert a random int between min and max for each index
  for i := 0; i < length; i++ {
    arr[i] = rand.Intn(max - min + 1) + min
  }

  return arr
}

// function which takes any number of ints and will return the minimum value from all of them
func minInt (nums... int) int {
  // declare min value as highest possible int
  min := math.MaxInt

  // if no values to compare we know min is already set to an unreasonable number
  if len(nums) == 0 {
    return min
  }
  
  // for all index (not used) and num in nums, if the current number is less than min, we found a new min
  for _, num := range(nums) {
    if num < min {
      min = num
    }
  }

  return min
}

// function to merge two halves of an array based on the indeces defining left and right halves
func mergeIterative(list []int, left, mid, right int) {
  // declare number of elements on left and right side
  numLeft := mid - left + 1
  numRight := right - mid

  // declare temporary arrays and populate them with values from original array
  leftArr := make([]int, numLeft)
  rightArr := make([]int, numRight)

  for i := 0; i < numLeft; i++ {
    leftArr[i] = list[left + i]
  }
  for i := 0; i < numRight; i++ {
    rightArr[i] = list[mid + i + 1]
  }

  // declare indeces for left and right arrays and where in original array to override the values
  leftIndex, rightIndex, mergedIndex := 0, 0, left

  // while both arrays have values, merge in the smaller of the two leading ones
  for leftIndex < numLeft && rightIndex < numRight {
    if(leftArr[leftIndex] <= rightArr[rightIndex]) {
      list[mergedIndex] = leftArr[leftIndex]
      leftIndex++
      mergedIndex++
    } else {
      list[mergedIndex] = rightArr[rightIndex]
      rightIndex++
      mergedIndex++
    }
  }

  // once one array runs out of values, merge all remaining values into original array
  for leftIndex < numLeft {
    list[mergedIndex] = leftArr[leftIndex]
    mergedIndex++
    leftIndex++
  }
  for rightIndex < numRight {
    list[mergedIndex] = rightArr[rightIndex]
    mergedIndex++
    rightIndex++
  }
  
}

// function to iteratively build up a sorted list based on the one provided
func mergeSortIterative(list []int) {
  // declare trivially sorted list which is of length 1 as already sorted
  sortedWidth := 1

  // get number of elements
  numElements := len(list)

  // while the length of the sorted array is less than the whole array there is work to do
  for sortedWidth < numElements {
    // always start leftmost sorted index at 0 in the array to build a bottom up solution
    leftIndex := 0
    // while the starting index is still within range of the array, merge halves of the array 
    for leftIndex < numElements {
      // declare right Index and mid value without indexing out of bounds on array
      rightIndex := minInt(leftIndex+sortedWidth*2-1, numElements-1)
      mid := minInt(leftIndex+sortedWidth-1, numElements-1)
      
      // merge two halves of the array defined by a left and right bound as well as a middle index
      mergeIterative(list, leftIndex, mid, rightIndex)

      // once halves are merged and therefore, sorted, we can move to next iteration which means leftIndex shifts by double the length of the currently sorted array size
      leftIndex += sortedWidth * 2
    }
    // when left index is out of bounds, we know the next phase of merging can begin, meaning we double the size of the sorted array width
    sortedWidth *= 2
  }
}

func main() {
  list := generateRandomIntegerArray(10, 0, 100)

  fmt.Printf("Before sorting: %v\n", list)

  mergeSortIterative(list)
  
  fmt.Printf("After sorting: %v", list)
}

// helper function for random integer array in range
function getRandomInt(min, max) {
  min = Math.ceil(min);
  max = Math.floor(max);
  
  return Math.floor(Math.random() * (max - min + 1)) + min;
}

function mergeIterative(array,left,mid,right) {
    // create temp arrays with values from array
    const rightArray = array.slice(left,mid + 1);
    const leftArray = array.slice(mid + 1,right + 1);
    
    // declare temp array index values to know which one to get value from
    let leftIndex = 0;
    let rightIndex = 0;
    let mergedIndex = left;
    
    // while temp arrays both have values, insert smaller values to array
    while(leftIndex < leftArray.length && rightIndex < rightArray.length) {
        if(leftArray[leftIndex] <= rightArray[rightIndex]) {
            array[mergedIndex] = leftArray[leftIndex];
            leftIndex += 1;
            mergedIndex += 1;
        } else {
            array[mergedIndex] = rightArray[rightIndex];
            rightIndex += 1;
            mergedIndex += 1;
        }
    }
    // merge all remaining values into array
    while(leftIndex < leftArray.length) {
        array[mergedIndex] = leftArray[leftIndex];
        leftIndex += 1;
        mergedIndex += 1;
    }
    while(rightIndex < rightArray.length) {
        array[mergedIndex] = rightArray[rightIndex];
        rightIndex += 1;
        mergedIndex += 1;
    }
}

function mergeSortIterative(array) {
    // sorted subarray length starts at trivially sorted solution of one element
    let sortedArraySize = 1;
    // declare number of elements
    let numElements = array.length
    
    // while sorted part of array is not same length as array
    while (sortedArraySize < numElements) {
        // start left at 0 showing first index sorted trivially is left index
        let left = 0;
        // while we have not yet exhausted the possible leftmost index values for this iteration
        while(left < numElements) {
            let right = Math.min(left + (sortedArraySize*2 - 1), numElements - 1);
            let mid = Math.min(left + sortedArraySize - 1, numElements - 1);
            
            mergeIterative(array, left, mid, right);
            
            // left increases by double the currently sorted list to simulate halves being sorted
            left +=  sortedArraySize * 2;
        }
        // once this iteration is complete, we merge the next half which means doubling size of sorted list
        sortedArraySize *= 2;
    }
    
    return array;
}

// following code is main
let list = Array.from({length: 10}, () => getRandomInt(0,100));

console.log("Before merge:",list);

list = mergeSortIterative(list);

console.log("After merge:",list);

More To Learn

Different Sorting Algorithms for Different Situations

As mentioned earlier, there are many, MANY, algorithms that are out in the world. Each algorithm comes with its own set of pros and cons. With your understanding of Merge Sort, it’s time to compare these factors among various algorithms. A good developer can weigh factors of two or more separate options which in theory could work but one may be just better than the rest for some reason. Maybe Merge Sort is ideal because of the worst case runtime being guaranteed to not exceed O(n*log(n)). It could also be possible that something like the Quick Sort works best since datasets for your problem are expected to be smaller.

The point is, having just one tool in your belt doesn’t solve every problem. If it did, you wouldn’t need a belt and all the learning we do is for nothing. That doesn’t sound like as much fun. So always be sure to know your tools and be able to select which fits which job best.

In-Depth Look into Recursion

While we’ve covered implementing Merge Sort with recursion and briefly introduced recursion, there’s much more to explore in this complex concept. The world of recursion is notoriously difficult for many to fully comprehend. I know it was very difficult for me to understand at first, but with plenty of studying and research, I was able to get a firm grasp of the idea.

There are many excellent resources to look through such as this GeeksForGeeks post and many others. Consider YouTube videos if you love animations and more visuals to aid the learning process.

Conclusion

Having explored various aspects of Merge Sort, you are now equipped with enough knowledge to not only use it in your interview prep or coding, but you can begin the next step in your programming journey equipped with one more tool in your programming tool belt.

Best of luck!