The world of computer science is riddled with words that can be scary and hard to keep track of. I’m sure seeing the terms “Big O Notation” and “Algorithm Analysis” make it seem like a tough space just to even get started on, let alone understand. I thought the same thing on my first time hearing these terms among others we will explore, but with time and practice, I’ve been able to not only learn these concepts and how to apply them but I also picked up on some tricks to apply in hoping to make it easier for you to understand it as well.
What is Big O Notation?
While I hate to do it so early on, it’s important to get the mathematical definition out of the way as I think it provides important context for the programming application of it.
Let f(n) and g(n) be two functions defined in the realm of positive integers. We say that f(n) is Big O of g(n) if there exist positive constants C and k such that, for all n greater than or equal to k:
f(n) <= C * g(n)
In the above definition, f(n) would be the function or program you are analyzing with g(n) being a simpler function, which essentially defines the upper bound for the growth rate of f(n) based on how large n is.
Now, I know this is disgusting to try and break down let alone imagine understanding or applying often but it can be simplified greatly for an introduction level as something as simple as “After n exceeds some value k, there is a simple function g(n) which f(n) cannot grow faster than by some constant C”. Even further simplified, “There’s a simple function g(n) which acts as an upper bound for f(n) as n grows in size”.
Big O is typically considered in analyzing the worst case scenario of an algorithm. It’s easy for any of us to say “oh, my algorithm could finish in one step because I find the thing I’m looking for first try” but this doesn’t help us when it comes to analyzing algorithms for inputs that can be unpredictable or difficult to even visualize at times. This is part of why it is important to have a foundational understanding of Big O Notation. There will come a time in an interview, during a demonstration, or maybe in your own code optimization workflow, where seeing a worst case scenario and looking for a demonstrably better solution will be an invaluable skill to have and what better way to show that to others and yourself than to speak the language of it while being correct in your analysis and being able to optimize an algorithm to be quicker for larger inputs?
In summary, Big O tells us an upper bound for the runtime of our programs and functions. More examples still to be explored but it is worth noting that saying “A is Big O of Z” can be noted as “A is O(Z)” and I will be using both interchangeably throughout this article.
Common Big O Functions
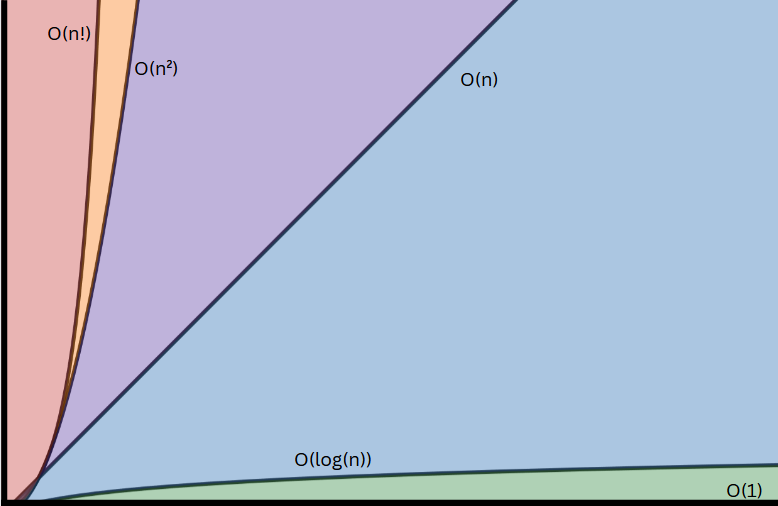
All of the following Big O functions will be listed in order of growth in relation to the size of the input, n, being passed into it as shown in the above graph which is helpful for visualizing the vast difference between many of these functions.
O(1)
Also known as “constant time”, this function is used to describe an algorithm which no matter how big the input becomes, the algorithm will complete in the same amount of time.
This nickname of “constant time” can mislead many because this doesn’t mean the algorithm is over quickly, “in no time at all”, “in a jiffy”, or “quicker than you can say algorithm analysis is a fun topic if you think about it”. It simply means the amount of time necessary to complete is not dependent on the size of the input at all and will remain somewhat constant. If you look at the graph above, you can see that the O(1) line remains low as we go along the x axis of the graph. Examples of this can be seen in the code samples below written in the C programming language.
int add(int a, int b) {
return a + b;
}
/*
O(1) because no matter how big the inputs get,
the function is completed in the same amount of steps
*/int mathOnFirstValue(int* array) {
if(array == null)
return 0;
int firstValue = array[0];
int firstValueAfterMath = firstValue * firstValue - 10 / 2 + 35;
return firstValueAfterMath * 2;
}
/*
despite this being several steps, it's important to
notice the same steps are repeated no matter how long
the array may be. Whether the array is of size 1 or
57326546, the number of steps will not change, making this O(1)
*/O(log(n))
Referred to as “logarithmic time”, this function describes the exponential decrease of runtime in relation to the size of the input to the function or algorithm. In the chart above we can see a slow upward inclination and that even the rate of change decreases as the size of the input increases. It is often characterized by the idea of “removing options” at a constant rate. The most common example is a binary search (more of this in a future article) in which you basically remove half of the possible choices with each decision.
To put how awesome this is into perspective, if the current input of a O(log(n)) function took 10 milliseconds to run with an input of 10 elements, it would take 20 milliseconds to process 20 elements, 30 milliseconds for an input of 40 elements, 40 milliseconds for an input of 80 elements, and so on. In this example, the base of the log function was two, given away by fact that the input can double with only a linear increase in the amount of time or steps needed to process it! The example below can help explain this idea best.
Guessing Games
You know the classic game, “I’m thinking of a number from 1 to 100, bet you can’t guess which it is”. While you know you can eventually reach it if you exhaust all 100 numbers by guessing or in order, it doesn’t seem ideal because it takes a long time to do. So you, being the excellent problem solver you are, bet that you can get it in less than 7 guesses if they tell you higher or lower. The most unlikely thing to happen is you got it right, but if you did then you win. The more likely possibilities is you’re told either higher or lower. We’ll say you’re told higher. You now know that any guesses from 1 to 50 would be pointless so you can count them out. BOOM! Half the problem gone with one guess. You now guess 75. Lower. Again, you removed half of your options with one more guess. In two guesses, you got from 100 options to 25 left. Not bad. You can keep this up and due to the power of logarithms, you know you can get to the right answer within 7 guesses since log2(100) = 6.643, rounded up to 7 because you can’t do 0.643 of a guess. If you can, you might be cheating but the important takeaway here is the fact that each extra action or choice meant removing a portion of your future possible options; an important pattern to recognize for functions that are O(log(n)).
O(n)
Often referred to as “linear time” function mostly attributed to the fact that the runtime is positively correlated with the size of the input and will therefore grow linearly. A good pattern to look for in order to know an algorithm is O(n) would be if you can describe it as a “look through all elements” algorithm or a “(possibly) for all” algorithm. The following segments of code show some examples of O(n) algorithms.
private static int totalSum(int[] array) {
if (array == null)
return 0;
int sum = 0;
for (int i = 0 ; i < array.length ; i++) {
sum += array[i];
}
return sum;
}
/*
O(n) because of the notable pattern indicating
a "for each element of the array" idea. A for loop
through the input is typically a good indicator of
a function being O(n)
*/public int productExceptFive(int[] array) {
if (array == null)
return 0;
int product = 1;
for (int index = 0 ; index < 5 ; index++) {
if (array[index] == 5)
return 0;
product *= array[index];
}
return product;
}
/*
O(n) because despite possibly getting cut short,
it is possible in the worst case, that it actually
returns the product of all n integers in the array
*/O(n²)
Up next is the “quadratic time” function characterized by the rapid growth of runtime in relation to the input size. We can typically tell a function is O(n²) if there appears to be a pattern that can be described as “for each element, look through all elements”. We could break it down as a O(n) algorithm n times, which helps us see why the rate of growth is so large. Each extra element becomes n extra actions to complete which leads to exponential growth in runtime. Some sample code showing O(n²) functions can be seen below.
function mysterious(sentence: string[]): number {
if (!sentence)
return 0;
let total = 0;
for (let i = 0; i < sentence.length; i++) {
for (let j = i + 1; j < sentence.length; j++) {
if (sentence[i] === sentence[j]) {
total++;
}
}
}
return total / 2;
}
/*
common O(n²) pattern because we see that for each
iteration of the outer for loop, we do another iteration
through the array for the inner for loop, this can be
seen as O(n) functions, n times resulting in O(n*n) => O(n²)
*/function bubbleSort(arr: number[]): number[] {
if (!array){
return [];
}
const n = arr.length;
for (let i = 0; i < n - 1; i++) {
for (let j = 0; j < n - 1 - i; j++) {
if (arr[j] > arr[j + 1]) {
const tmp = array[j];
array[j] = array[j + 1];
array[j + 1] = tmp;
}
}
}
return arr;
}
/*
a classic sample of Bubble Sort! A shining example
of O(n²) because again, we see a pattern of looping
the length of our array the same amount of times as
the length of the array to begin with
*/O(n!)
Big O “n factorial”, it is even more inefficient than the O(n²) algorithms because one extra element of input does not mean adding n more steps, it means multiplying by n steps.
The factorial of a number is described as the product of all numbers between one and itself. For example, the factorial of 5 is 5 * 4 * 3 * 2 * 1 which is equal to 120. Imagine processing 5 elements taking 120 repeated steps and then we can start to see how bad this is considering that adding a sixth element would make our algorithm complete in 120 * 6 steps which is 720.
This realm of Big O is where a lot of inefficient algorithms can be placed and it is rarer to find algorithms in this range, but it always helps to see an example.
Permutations
You’re given the task of generating all possible permutations of an array. So naturally, you look up the definition of a permutation and learn that it is essentially an arrangement of elements in some list and then you realize generating all permutations of an array can take a long time. Consider just the string ‘ABC’, all permutations of this would be: ‘ABC’, ‘ACB’, ‘BAC’, ‘BCA’, ‘CAB’, and ‘CBA’. That’s six (6) permutations from 3 characters. Some deeper analysis leads us to see the factorial at play. A string of length 3 results in 6 permutations, that’s 3 * 2 * 1 permutations! A string of 4 can be predicted then to be 4 * 3 * 2 * 1 which is 24.
Some more reasoning on this is in order to do all permutations, you need to first cycle through all n characters and fix them as the first character at some point. While you have your first character, you need to cycle through all n-1 leftover characters as second character in the string and so on. We then get a loop where we have n * (n-1) * (n-2) * … * 1. The definition of a factorial!
Personal note: I’m content with myself because I programmatically wrote out all of those permutations from my head using the algorithm described previously.
Achieving Simple Functions
Having seen many of the common Big O functions and some examples, I’m sure it would be nice if all algorithms were that straight forward. Sadly, they’re not. So we need some rules on how to effectively and concisely communicate our algorithm analysis to others because there’s no fun in saying “my algorithm actually runs in O(n² + 10 * h + n + 64756536) time”.
Thankfully, two simple rules help us make communicating these ideas quick and easy:
- Drop Constants
- With Big O being an upper bound measuring tool, we don’t need to worry about one function being faster than another by a constant number of steps or a constant factor that doesn’t grow along with the input
- Ignore Non-Dominant Terms
- In cases where we know one term will grow faster than another, we simply shift focus onto that because sure in the scales of 10s maybe 100s some of those differences matter but when you get into millions and billions, those terms get overshadowed by a lot
- Something to remember with this rule is not all terms can be ruled out because we simply don’t know their relationship to other terms
We can see these rules in action with the following examples of functions being simplified for Big O notation
- O(n² + n + 25) => O(n²)
- n² is clearly going to outgrow n and a constant of 25 needs to be dropped regardless
- O(25 + 100 + 35) => O(1)
- no matter how big the input gets for this algorithm, the number of steps is constant
- O(n * log(n))
- This function is in simple form because despite the n outpacing the log(n) for growth, they are directly linked and the growth of one will definitely lead to the growth in the other
- O(n³ * n⁴ + n²) => O(n⁷ + n²) => O(n⁷)
- Note here the importance of dominant terms. The n³ and n⁴ terms are linked and their product will clearly outgrow the n² term
- O(2h + 10k + 38d) => O(h + k + d) or O(max(h,k,d))
- When dealing with algorithms that can take input from various sources or where the algorithm’s performance depends on several factors which can’t be predicted by any measure, it’s nice to be able to address those concerns in your analysis. Here, there are three factors to consider, each rising at a linear rate. They must all be a part of our final result since we cannot determine which is the dominant term in this function.
- O(35h + 146754692k + d*log(d)) => O(d*log(d))
- Similar to the prior example, there’s three factors which we cannot determine the largest value from. Key difference is one factor, no matter the size, grows faster than the others and that is d*log(d) since we can remove the constants from the h and k factors.
Space AND Time?
Until now, we’ve discussed analysis of algorithm runtime or number of steps to complete. This isn’t the only application of Big O though, because we can use it to measure the amount of space an algorithm would need as well.
All of the rules of the functions remain the same here but the key difference is to consider if the amount of memory being used to solve the problem grows in relation to the input. An example here is the Counting Sort algorithm which is limited to use on integer arrays but is completed by making an array the size of the largest value in an array and loops through the input array, incrementing the index of the corresponding index on the created array. In the end, the resulting array is made by inserting the index number as many times as its resulting value. An example is provided below.
#include <stdio.h>
#include <stdlib.h>
int lengthOfArray(int arr[]) {
int length = 0;
for(int i = 0; arr[i] != '\0'; i++){
length++;
}
return length;
}
void countingSort(int* array) {
if(array == NULL) {
return;
}
int length = lengthOfArray(array);
// find largest number in array
int max = array[0];
for(int i = 0; i < length; i++){
if(array[i] > max){
max = array[i];
}
}
// create count array
int* maxLengthArray = (int*) malloc((max + 1) * sizeof(int));
for(int i = 0; i < length; i++){
maxLengthArray[array[i]]++;
}
//print resulting array (could return but will just print it)
for(int i = 0; i < max + 1; i++){
for(int j = 0; j < maxLengthArray[i]; j++){
printf("%d ", i);
}
}
}
int main(void) {
int* array = malloc(sizeof(int) * 5);
array[0] = 2;
array[1] = 70;
array[2] = 2;
array[3] = 100;
array[4] = 102;
countingSort(array);
}This section of code is tough to interpret but we can note a few things about this code with what we’ve learned:
- lengthOfArray function is O(n) runtime because we iterate through the entire array to the end, seeing each index of it, before returning the final value but also doesn’t allocate any extra memory so it’s space complexity is O(1)
- countingSort function has a time complexity of O(n+n+k) (in order of steps) which simplifies to O(n+k) or O(max(n,k)) by removing the constant of 2 from the n factors which get added together. We need to define each of these, n is the length of the array and k is the largest number in the array. We can’t reliably say which will affect the runtime more but we know they are both crucial to analyzing the runtime of the algorithm
- countingSort does some memory allocation or creation of a data structure on line 30 so it’s important to notice that the size of this array is always the size of the largest number in array, which we have defined as k. Therefore, the space complexity of this Counting Sort implementation is O(k) since the number of elements in our input doesn’t affect this outcome
Seeing this, we continue to see patterns of analysis in space complexity that were established in time complexity. One trick I use to remember the slight difference is by framing it as “how much EXTRA memory does my algorithm need in order to be successful?”. This way, it’s clear that the array takes up space but Big O for space complexity is worried about the memory we create while processing that input.
More to Learn
Great, we’ve covered these several examples of Big O functions and ways to communicate with it but now what? I can confidently say that with this article alone, neither of us is a pro when it comes to Big O analysis. We have a lot to learn. Thankfully, there’s several points below that will help guide us on that journey.
Analyzing Code
Seeing the examples of code above is not enough to be able to confidently say you know Big O. Feel free to look around and find samples of code to analyze, quiz yourself wherever possible, and take time to analyze your own code and see what interesting patterns you find in your own algorithms and functions.
There is an awesome set of practice problems hosted on Kodr, where you can get practice analyzing code to see if you can find their Big O runtime.
Optimizing Code
After analyzing code, you get to a cool point where you can actually look for ways to optimize your code or code from others. Seeing that something is O(n) when it could be O(log(n)) whether it’s in space or time will be so rewarding to spot and even more rewarding to optimize.
This comes with practice so don’t be scared to revisit some old code, analyze it, and find some weak points in it which you can improve.
Other Notations
I can happily report that Big O is not the end of your algorithm analysis journey. There are it’s sibling notations Big Omega (Ω) and Big Theta (Θ), each with their own purpose and applications. I’m hoping to get an article on these out soon but in the meantime feel free to look around and read up on these if you have the time.
Conclusion
Being able to analyze and optimize code in terms of runtime and space usage is a valuable skill to have and will improve your ability to write not just any algorithm but an effective one. An understanding of this concept will improve your discussion on and understanding of algorithms and data structures. On top of that, questions on Big O concepts come up in technical interviews quite often so make sure to make use of this skill as often as you can.
Best of luck in your algorithm analysis and optimization journey!

